Problemas Resueltos de Electrostatica

Problema 6

 Esferas cargadas

dificultad

 

Dos esferas igualmente cargadas de 250 g de masa se encuentran suspendidas cada una de ellas por un hilo que cuelga del mismo punto del techo. Sabiendo que los hilos miden cada uno 75 cm y forman un angulo de 25º con la vertical, calcular:

a) ¿Cuál es la fuerza con la que se repelen las cargas?
b) ¿Cuál es el valor de las dos cargas?

(Datos: K = 9·10⁹ N·m²/C²)

Solución

Cuestión a)
Datos
m₁ = m₂ = 250 g = 0.25 Kg
L₁ = L₂ = 75 cm = 0.75 m
α = 25º
K = 9·10⁹ N·m²/C²
Resolución
Para resolver esta cuestión, vamos a realizar el diagrama de cuerpo libre de una de las esferas (en concreto m₂) y determinar que fuerzas intervienen en ella.

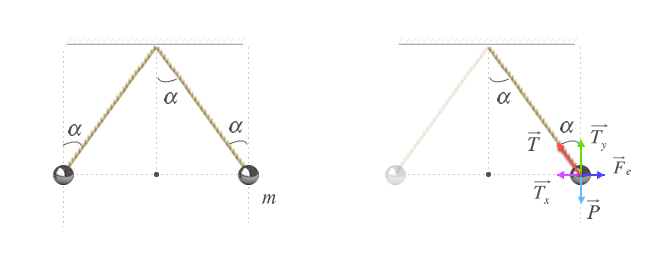Las fuerzas que intervienen en m₂ son:

• La tensión de la cuerda (T) que se puede descomponer en dos fuerzas T_x y T_y tal y como vimos en el apartado de descomposición de fuerzas, para que coincidan con los ejes de nuestro sistema de referencia.
• El peso (P) de la esfera.
• La fuerza eléctrica (F_e) de repulsión que hace que la esfera se separe de la vertical.

 Si aplicamos el principio fundamental o segunda ley de Newton a cada uno de los ejes del sistema de referencia, sabiendo que la esfera se encuentra en reposo en cualquiera de los ejes (a_x=0, a_y=0), obtenemos que:
Eje x

∑Fx=m2⋅ax ⇒Fe−Tx=m2⋅0 ⇒Fe=Tx

Sabemos que la fuerza eléctrica de repulsión es igual que la tensión en el eje x, pero ¿cuanto vale esta tensión?. Si aplicamos la definición del seno y coseno no solo calcularemos T_x si no también T_y.

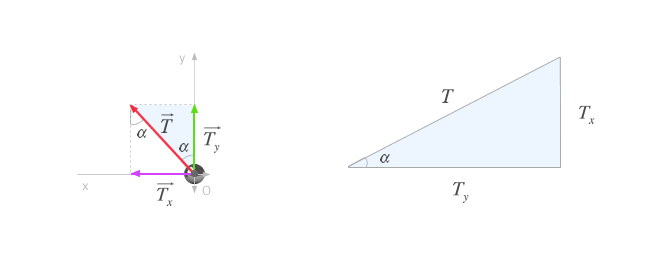Aplicando la definición de seno:

sin(α)=cateto opuestohipotenusa ⇒sin(α)=TxT ⇒Tx = T⋅sin(α)

Aplicando la definición de coseno:

cos(α)=cateto contiguohipotenusa ⇒cos(α)=TyT ⇒Ty = T⋅cos(α)

Por tanto, obtenemos que:

Fe=T⋅sin(α)

Eje y

∑Fy=m⋅ay ⇒Ty−P=m⋅ay ⇒T⋅cos(α)−m2⋅g = m2⋅ 0 ⇒T =m2⋅gcos(α) ⇒T=0.25⋅9.8cos(25)⇒T=2.70 N

Sustituyendo el valor de T en la primera ecuación podremos calcular el valor de la fuerza de repulsión:

Fe=T⋅sin(α) ⇒Fe = 2.70⋅sin(25) ⇒Fe=1.14 N

Cuestión b)
Conociendo el valor de la fuerza de repulsión Fe = 1.14 N, podemos aplicar la ley de Coulomb para conocer el valor de carga (q) de cada esfera, sabiendo que las dos tienen la misma:

Fe=K⋅q⋅qr2 ⇒Fe=K⋅q2r2⇒q=Fe⋅r2K−−−−−−√

Sabemos el valor de K y el de F_e sin embargo desconocemos la distancia entre las dos esferas. Para calcularla haremos de nuevo uso de la definición de seno aplicándola sobre el triángulo rectángulo que se forma entre la cuerda y la vertical.

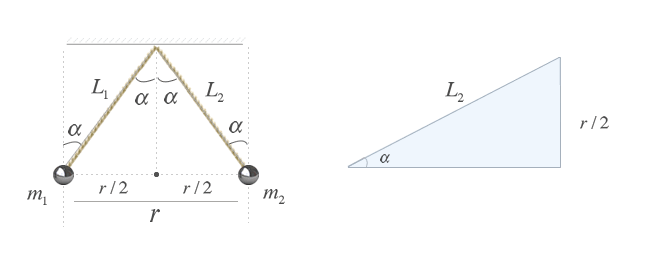
sin(α)=r/2L2⇒r=2⋅L2⋅sin(α) ⇒r=2⋅0.75⋅sin(25) ⇒r=0.63 m

Una vez que disponemos de todos los datos, el valor de la cargas es:

q=Fe⋅r2K−−−−−−√ ⇒q=1.14⋅(0.63)29⋅109−−−−−−−−−−−√ ⇒q=7.09⋅10−6 C

Dado que la fuerza eléctrica es de repulsión, el resultado que hemos obtenido nos dice que o bien las cargas son q₁=q₂=7.09·10^-6 C o q₁=q₂=-7.09·10^-6 C.

---