El campo eléctrico
El campo eléctrico (en unidades de voltios por metro) se define como la fuerza (en newtons) por unidad de carga (en coulombs). De esta definición y de la ley de Coulomb, se desprende que la magnitud de un campo eléctrico E creado por una carga puntual Q es:
La ley de Gauss
La ley de Gauss establece que el flujo eléctrico total a través de una superficie cerrada es proporcional a la carga eléctrica total encerrada dentro de la superficie. La constante de proporcionalidad es la permitividad del vacío.
Matemáticamente, la ley de Gauss toma la forma de una ecuación integral:
Alternativamente, en forma diferencial, la ecuación es:
La ecuación de Poisson
La definición del potencial electrostático, combinada con la forma
diferencial de la ley de Gauss, provee una relación entre el potencial Φ
y la densidad de carga ρ:
Esta relación es una forma de la ecuación de Poisson.
Ecuación de Laplace
En ausencia de carga eléctrica, la ecuación es
que es la ecuación de Laplace.



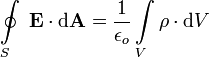


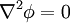
No hay comentarios:
Publicar un comentario