Problemas Resueltos de Electrostática
Problema 7
Ley de Coulomb con Más de Dos Cargas
Un sistema de 3 cargas
Enunciado
dificultad
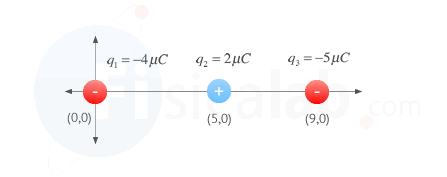
 Dado el sistema de cargas de la figura, determina la fuerza que experimenta q2 sabiendo que las tres cargas se encuentran en el vacío y el sistema de referencia está expresado en metros.
Dado el sistema de cargas de la figura, determina la fuerza que experimenta q2 sabiendo que las tres cargas se encuentran en el vacío y el sistema de referencia está expresado en metros.
Solución
Datos
q1 = -4 µC = -4·10-6 C
q2 = 2 µC = 2·10-6 C
q3 = -5 µC = -5·10-6 C
K = 9·109 N·m2/C2
Distancia entre q1 y q2. d1,2 = 5 m
Distancia entre q3 y q2. d3,2 = 9 - 5 = 4 m
Resolución
Aplicando el principio de superposición de fuerzas eléctricas, la fuerza (F⃗ 2 ) que actúa sobre q2 será la suma vectorial de:
- la fuerza que ejerce q1 sobre q2 (
F⃗ 1,2 ). Como q1 y q2 tienen distinto signo, F⃗ 1,2 será atractiva.
- la fuerza que ejerce q3 sobre q2 (
F⃗ 3,2 ). Como nuevamente q2 y q3 tienen distinto signo, F⃗ 3,2 será atractiva.
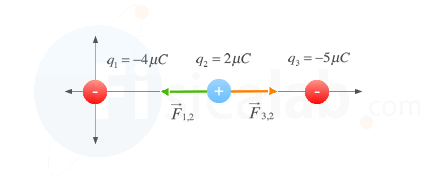
F⃗ 2=F⃗ 1,2+F⃗ 3,2
Vamos a estudiar F⃗ 1,2 y F⃗ 3,2 por separado:
Fuerza F⃗ 1,2
Aplicando la ley de Coulomb sobre las cargas q1 y q2 obtenemos que:
F⃗ 1,2=K⋅q1⋅q2d1,22⋅u⃗ 1,2
Por definición, u⃗ 1,2 es un vector unitario que tiene la misma dirección que la fuerza y el mismo sentido si q1 y q2
tienen el mismo signo y sentido opuesto si tienen signo distinto. En
nuestro caso el signo es distinto, por lo que será un vector unitario
que va en dirección y sentido del eje x.
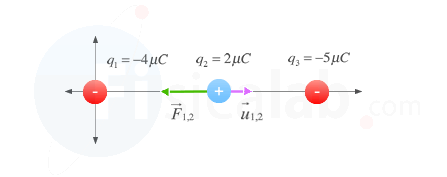
¿Ese vector te suena de algo?. Probablemente si, se trata del vector i o ux. Por tanto, u⃗ 1,2 =i⃗ :
F⃗ 1,2=K⋅q1⋅q2d1,22⋅i⃗ ⇒F⃗ 1,2=9⋅109⋅−4⋅10−6⋅2⋅10−652⋅i⃗ ⇒F⃗ 1,2 = −2.88⋅10−3⋅i⃗ N
Fuerza F⃗ 3,2
Al igual que con F1, vamos a utilizar la ley de Coulomb, pero esta vez para estudiar la fuerza que ejerce q3 sobre q2:
F⃗ 2,3=K⋅q3⋅q2d2,32⋅u⃗ 3,2
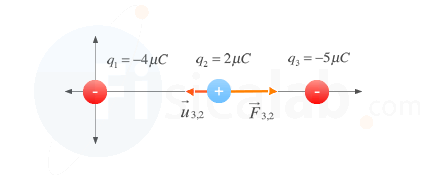
En este caso u⃗ 3,2 es precisamente el opuesto del vector i⃗ , ya que "mira" en sentido opuesto al eje x. Por tanto:
F⃗ 2,3=K⋅q3⋅q2d2,32⋅(−i⃗ ) ⇒F⃗ 2,3=9⋅109⋅−5⋅10−6⋅2⋅10−642⋅(−i⃗ ) ⇒F⃗ 2,3=−5.62⋅10−3⋅(−i⃗ ) ⇒ F⃗ 2,3=5.62⋅10−3⋅i⃗ N
F⃗ 2=F⃗ 1,2+F⃗ 3,2 ⇒F⃗ 2=−2.88⋅10−3⋅i⃗ + 5.62⋅10−3⋅i⃗ ⇒F⃗ 2=2.74⋅10−3⋅i⃗ N
F⃗ 2=F⃗ 1,2+F⃗ 3,2 ⇒F⃗ 2=−2.88⋅10−3⋅i⃗ + 5.62⋅10−3⋅i⃗ ⇒F⃗ 2=2.74⋅10−3⋅i⃗ N
Enunciado
dificultad
Dado el sistema de cargas de la figura, determina la fuerza que experimenta q2 sabiendo que las tres cargas se encuentran en el vacío y el sistema de referencia está expresado en metros.

Solución
Datos
q1 = -4 µC = -4·10-6 C
q2 = 2 µC = 2·10-6 C
q3 = -5 µC = -5·10-6 C
K = 9·109 N·m2/C2
Distancia entre q1 y q2. d1,2 = 5 m
Distancia entre q3 y q2. d3,2 = 9 - 5 = 4 m
Resolución
Aplicando el principio de superposición de fuerzas eléctricas, la fuerza (F⃗ 2 ) que actúa sobre q2 será la suma vectorial de:
q1 = -4 µC = -4·10-6 C
q2 = 2 µC = 2·10-6 C
q3 = -5 µC = -5·10-6 C
K = 9·109 N·m2/C2
Distancia entre q1 y q2. d1,2 = 5 m
Distancia entre q3 y q2. d3,2 = 9 - 5 = 4 m
Resolución
Aplicando el principio de superposición de fuerzas eléctricas, la fuerza (
- la fuerza que ejerce q1 sobre q2 (
F⃗ 1,2 ). Como q1 y q2 tienen distinto signo,F⃗ 1,2 será atractiva. - la fuerza que ejerce q3 sobre q2 (
F⃗ 3,2 ). Como nuevamente q2 y q3 tienen distinto signo,F⃗ 3,2 será atractiva.

Fuerza
Aplicando la ley de Coulomb sobre las cargas q1 y q2 obtenemos que:

¿Ese vector te suena de algo?. Probablemente si, se trata del vector i o ux. Por tanto,
Al igual que con F1, vamos a utilizar la ley de Coulomb, pero esta vez para estudiar la fuerza que ejerce q3 sobre q2:

En este caso
F⃗ 2=F⃗ 1,2+F⃗ 3,2 ⇒F⃗ 2=−2.88⋅10−3⋅i⃗ + 5.62⋅10−3⋅i⃗ ⇒F⃗ 2=2.74⋅10−3⋅i⃗ N
No hay comentarios:
Publicar un comentario